1. Funciones Trigonométricas Fundamentales
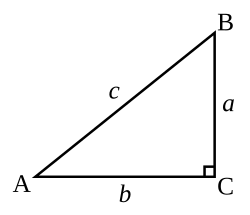
Definición Geométrica
En un triángulo rectángulo, las funciones trigonométricas se definen como razones entre sus lados:
Seno (sen)
Relación entre el cateto opuesto al ángulo y la hipotenusa:
\[ \sin \theta = \frac{\text{Longitud del cateto opuesto}}{\text{Longitud de la hipotenusa}} \]Características:
- Rango: [-1, 1]
- Cero en múltiplos de π
- Máximo absoluto en π/2 (90°)
Coseno (cos)
Relación entre el cateto adyacente al ángulo y la hipotenusa:
\[ \cos \theta = \frac{\text{Longitud del cateto adyacente}}{\text{Longitud de la hipotenusa}} \]Propiedades:
- Función par: cos(-θ) = cos θ
- Relacionado con posición horizontal en el círculo unitario
- Fase desplazada π/2 respecto al seno
Tangente (tan)
Relación entre el cateto opuesto y el adyacente:
\[ \tan \theta = \frac{\sin \theta}{\cos \theta} = \frac{\text{Opuesto}}{\text{Adyacente}} \]Comportamiento único:
- Asíntotas verticales en π/2 + kπ
- Período π (180°)
- Amplio uso en pendientes e inclinaciones
¿Por qué son importantes?
Estas funciones permiten modelar fenómenos periódicos y relaciones angulares en:
- Física: Movimiento armónico, ondas
- Ingeniería: Diseño estructural, circuitos
- Astronomía: Cálculo de distancias estelares
- Computación Gráfica: Rotaciones 3D
2. El Círculo Unitario: Una Revolución Conceptual

De Triángulos a Coordenadas
El círculo unitario (radio = 1) generaliza las funciones trigonométricas para cualquier ángulo:
\[ \begin{align*} \text{Coordenada } x &= \cos \theta \\ \text{Coordenada } y &= \sin \theta \\ \text{Pendiente} &= \tan \theta \end{align*} \]Paso 1: Considera un ángulo θ en posición estándar
Paso 2: Dibuja el triángulo rectángulo formado por: \[ \text{Hipotenusa} = 1 \quad (\text{radio}) \]
Paso 3: Por definición de seno y coseno: \[ \cos \theta = \frac{\text{adyacente}}{1} = x \] \[ \sin \theta = \frac{\text{opuesto}}{1} = y \]
Conclusión: Las coordenadas (x,y) corresponden exactamente a (cos θ, sin θ)
Cuadrantes y Signos
| Cuadrante | sin θ | cos θ | tan θ |
|---|---|---|---|
| I | + | + | + |
| II | + | - | - |
| III | - | - | + |
| IV | - | + | - |
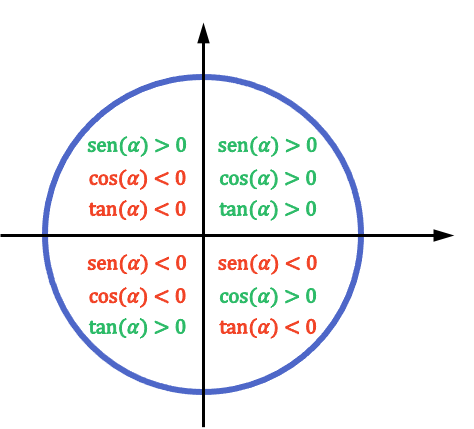
Regla mnemotécnica: "Todos Sentimos Tantas Cosas". Esto nos sirve para recordar qué funciones son positivas en cada cuadrante.
3. Aplicaciones en el Mundo Real
Ejemplo 1: Altura de un Edificio
Problema: Determinar la altura de un rascacielos usando un teodolito que mide un ángulo de elevación de 65° desde 100 metros de distancia.
Solución usando tangente:
\[ \tan 65^\circ = \frac{\text{Altura}}{100\ m} \Rightarrow \text{Altura} = 100 \times \tan 65^\circ \approx 214.5\ m \]Ejemplo 2: Análisis de Circuitos
En corriente alterna, el voltaje sigue una función senoidal:
\[ V(t) = V_{\text{max}} \sin(2\pi f t) \]Donde:
- \(V_{\text{max}}\) = Voltaje máximo
- \(f\) = Frecuencia en Hertz
- \(t\) = Tiempo en segundos
Curiosidad Histórica
Las primeras tablas trigonométricos fueron calculadas por Hiparco de Nicea (190-120 a.C.) para aplicaciones astronómicas. Sus tables contenían valores de cuerdas (equivalentes al doble del seno) para ángulos en incrementos de 7.5°.